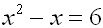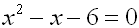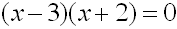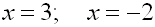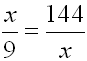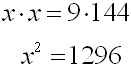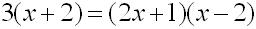Solving Quadratic Equations
An Example Of A Math Lesson In English

(A quadratic equation is a polynomial equation of degree two.
The standard form is  ax2 + bx + c = 0.)

  

Ok.. There are primarily three types of factoring:

  
*Common Monomial

ab + ac = a(b + c)

*Difference of Squares x2 - 9 = (x +3)(x - 3)
*Quadratic Trinomial x2 - 5x + 6 = (x - 3)(x - 2)

If you can factor, you will be able to solve factorable quadratic equations.
Let's see how it is done.
 

Solve for x:   

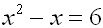
Here are the steps you should follow:

1. Move all terms to the same side of the equal sign, so the equation is set equal to 0.
This places the equation in standard form.
2. Factor the algebraic expression.
(x + 3) and (x + 2) are called factors.  These are factors of the expression
 x2 - x - 6.
3. Set each factor equal to 0.
(This process is called the "zero product property".  If the product of two factors equals 0, then either one or both of the factors must be 0.)
4. Solve each resulting equation.
x = 3  and  x = -2 are called roots.  These are roots of the equation x2 - x - 6 = 0.


 

Example 1

Solve for x:    x2 + 3x = 0

Factor the common monomial.             x(x + 3)=0
Set each factor equal to 0 and solve for x.

x = 0 

 x + 3 = 0
x = -3
List all values of x. x = {0, -3}

 

Example 2

Solve for y:     y 2 = 16

Get all terms on the same side.            y 2 - 16 = 0
Factor the difference of squares.         (y + 4)(y - 4) =0
Set each factor equal to 0 and solve for y.

y + 4 = 0
y = -4

 y - 4 = 0
y = 4
List all values of y. y = {-4, 4}

 

Example 3

Solve for c:   c 2 - 12 = c

Get all terms on the same side.           c 2 - 12 - c =0
Arrange the terms in standard form.           c 2 - c - 12 = 0
Factor the quadratic trinomial.          (c + 3)(c - 4) = 0
Set each factor equal to 0 and solve for c.

c + 3 = 0
c = -3

 c - 4 = 0
c = 4
List all values of c. c = {-3, 4}

 

Example 4

Solve for x: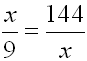    

Employ "product of the means = product of the extremes" (cross-multiply) for this proportion.
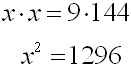Get all terms on the same side.     x 2 - 1296 = 0
Factor the difference of squares.        (x + 36)(x - 36) =0
Set each factor equal to 0 and solve for x.

x + 36 = 0
x = -36

x - 36 = 0
x = 36

List all values of x. x = {-36, 36}

 

Example 5

Solve for x:    

Employ "product of the means = product of the extremes" (cross-multiply) for this proportion. 
Get all terms on the same side.     0 = 2x 2 - 6x - 8
Factor the common monomial. 0 = 2(x 2 - 3x - 4)
Factor the quadratic trinomial.   2(x - 4)(x + 1) =0
Set each factor equal to 0 and solve for x.

x + 1 = 0
x = -1

List all values of x. x = {-1, 4}

 

Example 6

Write a quadratic equation, in the form  ax2 + bx + c = 0, whose roots are 2 and 5.

The simplest answer will be an equation where the factors of the expression are
(x - 2) and (x - 5).  Create this equation.		 (x - 2)(x - 5) = 0
Multiply.     x 2 - 5x - 2x + 10 = 0
Combine to get an answer equation. x 2 - 7x + 10 = 0

 

Example 7

The square of a number exceeds 5 times the number by 24.  Find the number(s).   

Translate the problem into a mathematical equation.  x2 = 5x + 24
Get all terms on the same side.     x 2 - 5x - 24 = 0
Factor the difference of squares.        (x - 8)(x + 3) =0
Set each factor equal to 0 and solve for x.

x - 8 = 0
x = 8

x + 3 = 0
x = -3

List all values of x. x = {8, -3}

 

Example 8

In football, the height of the football reached during a pass can be modeled by the equation  h = -16t 2 + 28t + 6, where the height, h, is in feet and the time, t, is in seconds.  How long does it take for this ball to reach a height of 12 feet?  

Substitute 12 into the equation for h. 12 = -16t 2 + 28t + 6
Get all terms on the same side.  Move terms to the left side to avoid working with a negative leading coefficient.     16t 2 - 28t + 6 = 0
Factor the quadratic trinomial.        (4t - 1)(4t - 6) =0
Set each factor equal to 0 and solve for t.

4t - 1 = 0
 4t = 1
t = 1/4
 

4t - 6 = 0
4t = 6
t = 6/4=3/2

List all values of t that are positive.  Negative time, should it appear, is not considered an answer. t = {1/4, 3/2}.  Reaches a height of 12 feet when time is 0.25 seconds (ball going up) and 1.5 seconds (ball coming down).